Geometric Model of a Bent Microtubule

Tom Goddard
August 2, 2013

Here is a Python Chimera 1.8 script microtubule.py that creates a model of a bent microtubule where each tubulin monomer is represented by a sphere.

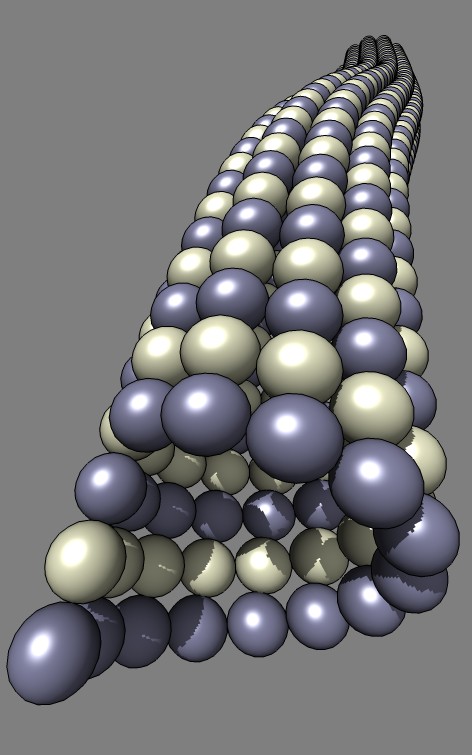
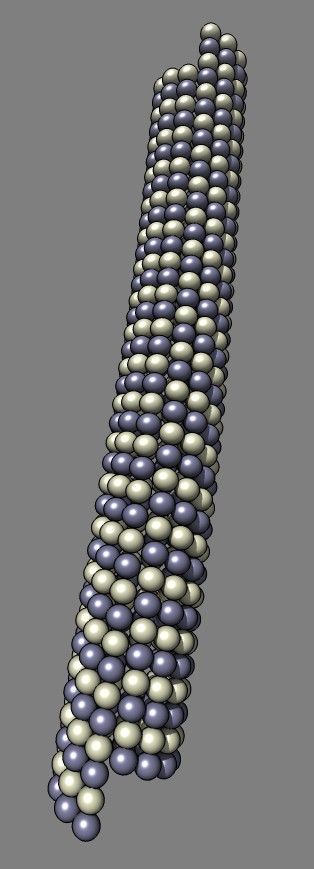
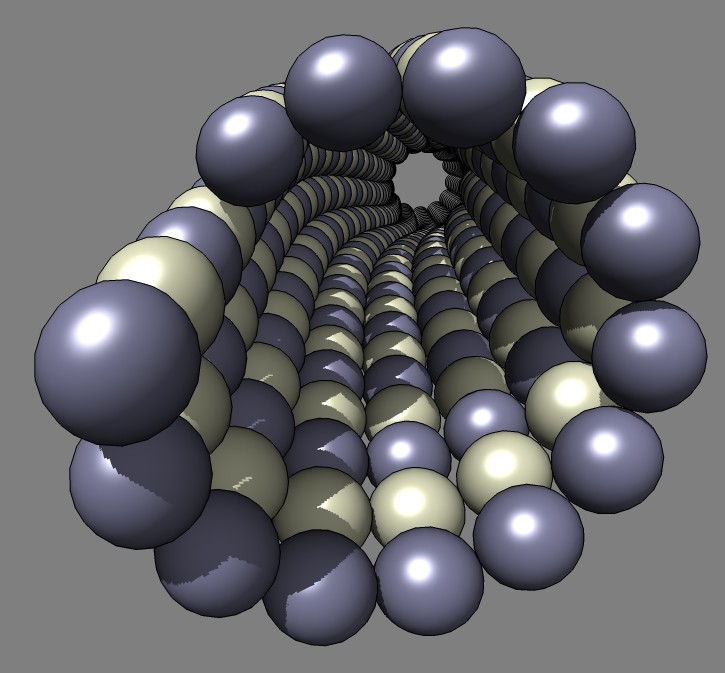
This example Python code was written for Misha Vysotskiy and Graham Johnson as a first step towards visualizing simulations of kinesin walking on 3-dimensional microtubules.

Details

• Cubic spline path. The center-line path of the microtubule is a natural cubic spline through a small number of points. A natural cubic spline has matching first and second derivatives at the specified points and zero second derivatives at the ends. There are 4 points explicitly specified at the bottom of the Python code in the test() routine that generated the model shown in the images.
• Tubulin spacing. Points spaced at 4 nanometer intervals were placed along the smooth path. The 4 nm spacing is the spacing of tubulin monomers in one of the 13 protofilaments.
• Center-line coordinate frames. A coordinate frame is placed at each of the points spaced at 4 nm. The z axis of each frame is tangent to the center line, with x and y axes perpendicular to the center line. There is continuity in the x and y axis directionsalong the path with the x and y axes of one point rotating onto the x and y axes of the frame at the next point about a rotation axis perpendicular to the plane of curvature of the path (at the first point).
• Tubulin monomer coordinate frames. Coordinate frames for each of the 13 tubulins in one helical turn are then made for each 4 nm point along the smooth path. The coordinate frame for the first tubulin is just the path point frame moved out by 9 nm along the x axis. The 9 nm is the radius of the microtubule measured from the center line to the centroid of a tubulin monomer. The other 12 tubulin coordinate frames of one helical turn are placed at 360/13 degree angular intervals and translated along the z-axis of the path point frame by 3 * 4 nm / 13 from one another to create a 3 tubulin monomer rise in one turn. These frames are rotated so the x-axis for a tubulin coordinate frame always points radially outward (ie perpendicular to the path point z-axis).
• Spheres. One sphere is placed for each tubulin frame. I stretched the sphere along the y-axis by 10 percent so the protofilaments appear to touch each other.

Notes

• Dimers versus monomers. It might make more sense to consider the basic subunit a tubulin dimer, since in reality it is a heterodimer consisting of alpha tubulin and beta tubulin. I built the model from monomers instead for simplicity.
• Seam. Because a helical turn rises 3 monomers while alpha tubulin and beta tubulins along a protofilament recur every 2 monomers, there is a seam in the microtubule. One pair of adjacent protofilaments has alpha tubulin side by side with beta tubulin while the other 12 pairs of neighboring protofilaments half alpha tubulin beside alpha tubulin, and beta tubulin beside beta tubulin.
• Tubulin atomic models. A tubulin surface or tubulin atomic model could be placed at each tubulin position instead of a sphere for more realism.
• Angstroms versus nanometers. The default parameters in the script are in Angstroms instead of nanometers so that atomic models (PDB models) which are in Angstroms will have the same scale as the microtubule model.
• Per-tubulin bending. Each helical turn of 13 tubulins is placed as a rigid unit using one of the path points. Sharper bends could be accomodated with better tubulin packing if instead each tubulin in the helical turn was placed using new path point coordinate frames spaced every 3 * 4 nm / 13 beginning at each 4 nm path point. The current approach allows no bend within one helical turn, while the fancier method would allow a single helical turn to distort to better follow the bend. In real microtubules I suspect the bend is so small because they are stiff, so it doesn't matter for most purposes.
• Handedness. The helical turns of real microtubules are left handed, so the example parameters are for a left handed helical turn.