
Tom Goddard
September 23, 2005
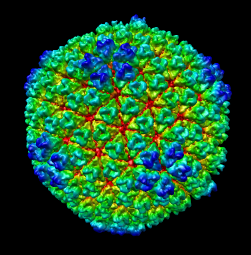
Comparison of virus capsid shapes to surfaces linearly interpolated between an icosahedron and a sphere.
The two examples show that if the interpolated surface is chosen to match the capsid envelope near 5-fold and 3-fold symmetry axes, then it protrudes further than the capsid near the 2-fold symmetry axes.

| 
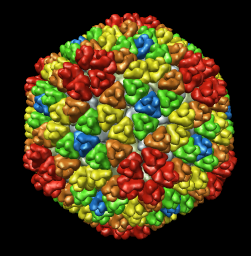
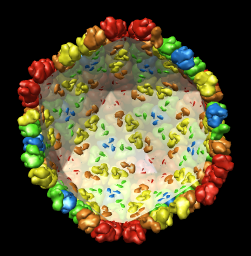
| Radial colored image: red = 300, yellow = 320, green = 340, cyan = 360, blue = 380 angstroms. Voxel size is 2.8 angstroms. |

| 
| 
| 
|

| 
| 
| 
|
| f = 0, r = 425 | f = 0.2, r = 400 | f = 0.5, r = 385 | f = 1, r = 360 |
f = interpolation factor between icosahedron and sphere, 0 = icosahedron, 1 = sphere.
r = radius of icosahedron to a 5-fold vertex (angstroms).
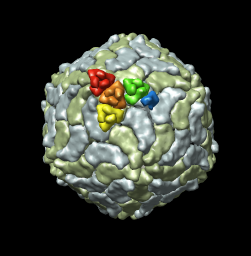
| 
| 
| 
|
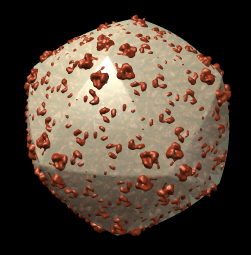
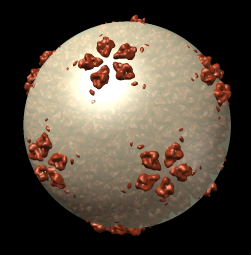
The inner and outer capsid layer in an atomic model of the rice dwarf capsid (PDB 1uf2) are not cleanly separated by the f = 0.2, r = 332 icosahedral surface. Proteins from both layers penetrate the surface.

|
Movie showing f = 0.2 surface colored according to EMD 1060 density maps at radii ranging from 2 to 430 angstroms in steps of 2 angstroms. Sample spacing is about 1.5 angstroms at largest radius. Colors from red to blue correspond to low to high density values. Blue = 6, cyan = 4, yellow = 2, red = 1, black = 0. |
Capsid envelope shape does not match any of the surfaces obtained by linearly interpolating an icosahedron and a sphere.

| 
| Radial colored image: yellow = 790, green = 835, cyan = 880, blue = 925 angstroms. |

| 
| 
| 
|

| 
| 
| 
|
| f = 0, r = 985 | f = 0.25, r = 930 | f = 0.5, r = 895 | f = 1, r = 820 |
f = interpolation factor between icosahedron and sphere, 0 = icosahedron, 1 = sphere.
r = radius of icosahedron to a 5-fold vertex (angstroms).